Le porte logiche sono gli elementi fondamentali dell'elettronica digitale, dunque di tutto cio' che comunemente si utilizza tutti i giorni (computer, smartphone, macchine fotografiche, videocamere) ma intese come "operatori logici" sono tra gli elementi fondamentali di ogni linguaggio di programmazione (esempio C, Java, PHP, Visual Basic), dunque di tutto il software che si utilizza comunemente (sistemi operativi Windows, Linux e Mac OS X, software da ufficio, fotoritocco, siti web dinamici ecc).
Tutte le porte logiche si basano sull'algebra di Boole.
Nella pratica è un'algebra che opera su espressioni logiche, dette, appunto, espressioni booleane, attraverso operatori logici che nel mondo elettronico si chiamano porte logiche e nel mondo informatico funzioni logiche.
Le porte logiche da considerare sono sette:
- NOT
- AND
- OR
- NAND
- NOR
- EX-OR
- EX-NOR
In sostanza le porte logiche eseguono delle operazioni logiche, ben distinte dalle operazioni aritmetiche, anche se in alcuni casi il risultato è lo stesso.
Esaminiamole una per una.
Porta NOT
La porta NOT è un operatore unario, nel senso che ha sempre un solo ingresso, che è una variabile binaria.
Come tutte le porte logiche ha una sola uscita.
La tavola della verità della porta NOT è la seguente
| A | Y |
|---|---|
| 0 | 1 |
| 1 | 0 |
Il significato è il seguente:
la porta logica NOT restituisce in uscita il negato (ossia il contrario) di quello che riceve in ingresso.
Il simbolo è il seguente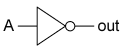
Fonte immagine: https://en.wikipedia.org/wiki/Inverter_%28logic_gate%29
in cui A è l'ingresso e Y=A' è l'uscita.
Il negato si puo' indicare con l'apice o con il sopralineato sopra la variabile A.
Porta AND
La porta AND è un operatore che puo' avere da due o più ingressi, che sono variabili binarie.
Come tutte le porte logiche ha una sola uscita.
La tavola della verità della porta AND è la seguente
| A | B | Y=AB |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Il significato è il seguente:
la porta logica AND restituisce in uscita il valore 1 solo se TUTTI gli ingressi sono pari a 1, altrimenti restituisce 0.
E' in sostanza il prodotto logico.
Il simbolo è il seguente
Fonte immagine: https://commons.wikimedia.org/wiki/File:AND_ANSI.svg
Porta OR
La porta OR è un operatore che puo' avere da due o più ingressi, che sono variabili binarie.
Come tutte le porte logiche ha una sola uscita.
La tavola della verità della porta OR è la seguente
| A | B | Y=A+B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Il significato è il seguente:
la porta logica OR restituisce in uscita il valore 1 solo se ALMENO uno degli ingressi è a 1, altrimenti restituisce 0.
E' in sostanza il somma logica, differente dalla somma aritmetica in binario, poiché non c'è riporto nel caso che gli ingressi sono tutti e due pari a uno.
Il simbolo è il seguente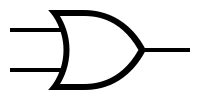
Fonte immagine: https://commons.wikimedia.org/wiki/File:OR_ANSI.svg
Porta NAND
La porta NAND è un operatore che puo' avere da due o più ingressi, che sono variabili binarie.
Come tutte le porte logiche ha una sola uscita.
La tavola della verità della porta NAND è la seguente
| A | B | Y=AB |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Il significato è il seguente:
la porta logica NAND restituisce in uscita il valore 0 solo se TUTTI gli ingressi sono pari a 1, altrimenti restituisce 1.
E' in sostanza il prodotto logico negato.
Il simbolo è il seguente
Fonte immagine: http://electronicsclub.info
Porta NOR
La porta NOR è un operatore che puo' avere da due o più ingressi, che sono variabili binarie.
Come tutte le porte logiche ha una sola uscita.
La tavola della verità della porta NOR è la seguente
| A | B | Y=A+B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Il significato è il seguente:
la porta logica NOR restituisce in uscita il valore 1 solo se TUTTI gli ingressi sono pari a 0, altrimenti restituisce 0.
E' in sostanza il somma logica, differente dalla somma aritmetica in binario, poiché non c'è riporto nel caso che gli ingressi sono tutti e due pari a uno, ma poi il risultato della somma viene negato.
Il simbolo è il seguente
Fonte immagine: https://commons.wikimedia.org/wiki/File:NOR_ANSI.svg
Porta EX-OR
La porta EX-OR è un operatore che puo' avere da due ingressi, che sono variabili binarie.
Come tutte le porte logiche ha una sola uscita.
La tavola della verità della porta EX-OR è la seguente
| A | B | Y= A ⊕ B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Il significato è il seguente:
la porta logica EX-OR restituisce in uscita il valore 1 solo se gli ingressi sono DIFFERENTI, altrimenti restituisce 0.
E' in sostanza un elogio della diversità.
Il simbolo è il seguente
Fonte immagine: http://electronicsclub.info
Porta EX-NOR
La porta EX-NOR è un operatore che puo' avere da due ingressi, che sono variabili binarie.
Come tutte le porte logiche ha una sola uscita.
La tavola della verità della porta EX-NOR è la seguente
| A | B | Y=A ⊕ B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Il significato è il seguente:
la porta logica EX-NOR restituisce in uscita il valore 1 solo se gli ingressi sono UGUALI, altrimenti restituisce 0.
E' in sostanza un elogio della uguaglianza.
Il simbolo è il seguente
Fonte immagine: http://electronicsclub.info
Le porte logiche
- AND
- OR
- NAND
- NOR
possono avere anche più di due ingressi.
Ecco qualche esempio:
Porta OR a tre ingressi
| A | B | C | Y=A+B+C |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Porta NAND a tre ingressi
| A | B | C | Y=ABC |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Porta NOR a quattro ingressi
| A | B | C | D | Y=A+B+C+D |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 |
